DIOPHANTIENNES (APPROXIMATIONS)

DIOPHANTIENNES (APPROXIMATIONS)

La théorie des approximations diophantiennes concerne principalement l’approximation des irrationnels par des rationnels. Dans le cas d’un seul irrationnel, un rôle essentiel est joué par les fractions continuées (utilisées dès 1650 par Huygens pour le calcul des engrenages des horloges astronomiques).

L’approximation des irrationnels algébriques fut étudiée par une méthode directe en 1844 par Liouville; ses résultats furent améliorés à de nombreuses reprises jusqu’à l’important et définitif résultat de Roth en 1955.

Dans le cas de plusieurs irrationnels, on peut soit chercher à approcher chacun d’eux par un rationnel, soit chercher à rendre minimale une forme linéaire à variables entières, à coefficients irrationnels (problème dual du précédent). Dans les deux cas, la théorie des réseaux de points (ou Z-modules, comme Zⁿ par exemple) joue un grand rôle, avec la caractérisation de ses bases et le théorème fondamental de Minkowski sur les domaines convexes symétriques d’un réseau ; ce dernier théorème conduit principalement à la résolution en entiers d’inégalités à coefficients irrationnels, ce qui est aussi un problème d’approximation diophantienne.

L’étude de la répartition modulo 1 a été également rattachée à cet article, étant encore, dans une certaine mesure, une question d’approximation diophantienne.

1. Z-modules et réseaux

Un Z-module de Rⁿ est un ensemble 紐 de points M de Rⁿ , de coordonnées (x ¹, x ², ..., x ⁿ ), qui est sous-groupe additif de Rⁿ (donc, s’il contient M et M , il contient u M + v M pour tout u et v de Z). On appelle base de 紐 un ensemble A¹, A², ..., A^r d’éléments de 紐, tel que tout élément de 紐 s’écrit, d’une manière unique, sous la forme a ¹A¹ + a ²A² + ... + a ^r A^r , où a ⁱ 捻 Z. On remarquera qu’on peut avoir r 礪 n (par exemple dans R avec les nombres de la forme a + b 連2, où a et b sont entiers, on a r = 2 pour n = 1).

Lorsque chaque point de 紐 est isolé dans Rⁿ , c’est-à-dire est centre d’une boule ne contenant pas d’autre point de 紐, le Z-module est dit discret ; cette propriété est évidemment caractérisée par le fait qu’il existe une boule de Rⁿ , de centre O, qui ne contient que O comme point de 紐. On appelle réseau tout Z-module discret et on démontre qu’un réseau de Rⁿ ne peut avoir de base comprenant plus de n éléments. Plus précisément, si un réseau admet une base de r éléments, l’espace vectoriel qu’il engendre est de dimension r .

Pour n = 1, tout réseau est donné par x = mx ⁰ où m 捻 Z et x ⁰ = inf |x | pour x 捻 紐 漣 O; en effet, 紐 étant discret, x ⁰ existe bien, est non nul et appartient à 紐, et tout x de 紐 en est multiple, sans quoi le reste du quotient de |x | par x ⁰ contredirait l’hypothèse faite sur x ⁰. Pour n quelconque, la démonstration de r 諒 n se fait par récurrence en projetant sur R^n-1 parallèlement à l’un des vecteurs OAⁱ .

On supposera, sans rien restreindre dans ce qui suit, que les réseaux envisagés correspondent à r = n . Un exemple fondamental est celui des points à coordonnées entières de Rⁿ , auquel on peut toujours se ramener dès qu’on a une base A¹, A², ..., Aⁿ du réseau: c’est Zⁿ .

Il est important de pouvoir caractériser les bases de Zⁿ ; on démontre qu’une condition nécessaire et suffisante pour que n points A¹, A², ..., Aⁿ de Zⁿ forment une base de ce réseau est que le déterminant de leurs coordonnées soit égal à 梁 1. Dans le cas de n = 2, si (p ¹, q ¹) et (p ², q ²) sont les coordonnées de A¹ et A², on doit donc avoir, pour une base, p ¹q ² 漣 p ²q ¹ = 梁 1, c’est-à-dire que les deux fractions p ¹/q ¹ et p ²/q ² sont adjacentes .

On remarque enfin que OA¹A² forment base de Z² si, et seulement si, le parallélogramme construit sur OA 轢¹, OA 轢² ne contient aucun point du réseau en son intérieur; il a alors pour surface 1, et cela se généralise à Zⁿ .

Un important théorème de Minkowski, sur les réseaux, sera vu plus loin.

2. Approximations d’un irrationnel. Fractions continuées

Dans le plan affine d’axes Ox , Oy , de vecteurs de base OA 轢, OB 轢, soit la demi-droite (OD) d’équation x = 精y , avec y 閭 0 et 精 捻 R. Approcher 精 par des rationnels p /q (avec q 礪 0) revient à approcher (OD) par des points du réseau de base OA 轢, OB 轢. Un point P(p , q ) de ce réseau est un point de voisinage à droite pour (OD) si p /q 礪 精 et 0 麗 p /q 漣 精 麗 p /q 漣 精 entraîne q 礪 q . Même définition à gauche avec 精 礪 p /q et 0 麗 精 漣 p /q 麗 精 漣 p /q . Un point P(p , q ) est un point réduit , relativement à (OD) si |p 漣 精 q | 麗 |p 漣 精 q | entraîne q 礪 q .

Si 精 est rationnel, soit 精 = u /v , la demi-droite (OD) porte le point entier P(u , v ) et il n’y a plus, au-delà de P, ni de point de voisinage, ni de point réduit pour (OD). Les points antérieurs à P sont donnés par le théorème suivant, qui s’applique sans limitation lorsque 精 est irrationnel: Si P^{n ,k} et P^{n, k+1} sont deux points de voisinage consécutifs (pour q croissant), d’un même côté de (OD), alors:

a ) La demi-droite portant le vecteur P^{n ,k} P^{n ,k+1}rencontre (OD) en un point Dⁿ⁺² (non entier).

b ) P^{n ,k} P^{n, k+h}= h P^{n, k} P^{n, k+1}donne, pour h = 1, 2, ..., les points de voisinage suivant P^{n, k} , du même côté de (OD), jusqu’au dernier avant Dⁿ⁺² , soit Pⁿ⁺² . Ces points sont adjacents deux à deux.

c ) OPⁿ⁺¹= P^{n, k} P^{n, k+1}et Pⁿ⁺² P^{n+1, 1}= P^{n, k} P^{n, k+1}donnent deux points de voisinages consécutifs, Pⁿ⁺¹ et P^{n+1, 1}, de l’autre côté de (OD), ce qui permet de poursuivre l’opération et d’obtenir tous les points de voisinage au-delà de P^{n, k} , sur deux lignes polygonales appelées lignes polygonales de Klein relatives à (OD); ces lignes forment enveloppe convexe des points entiers situés de part et d’autre de (OD).

d ) Seuls les sommets Pⁿ de ces lignes polygonales sont des points réduits.

Ce théorème s’établit par des considérations géométriques très élémentaires. On pose en général P^n-2 Dⁿ= 見ⁿ OP^n-1et P^n-2 Pⁿ= a ⁿ OP^n-1 轢; donc a ⁿ = [ 見ⁿ ], partie entière de 見ⁿ . La similitude des triangles OPⁿ Dⁿ et Dⁿ⁺¹ P^n-1 O donne alors 見ⁿ⁺¹ = 1/( 見ⁿ 漣 a ⁿ ) et l’on obtient ainsi, géométriquement, le développement en fraction continuée (régulière) de 精:

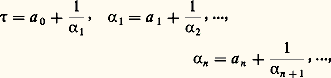avec a ⁰ = [ 精] et a ⁿ = [ 見ⁿ ]. Les 見ⁿ sont les quotients complets du développement et les a ⁿ , les quotients incomplets .

On écrit alors 精 = [a ⁰, a ¹, ..., a ^n-1 , 見ⁿ ] et p ⁿ /q ⁿ = [a ⁰, a ¹, ..., a ⁿ⁺¹ , a ⁿ ], n -nième réduite (qui correspond au point Pⁿ ), d’où:

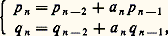ce qui exprime que P^n-2 Pⁿ= a ⁿ OP^n-1 轢. C’est grâce à ces formules de récurrence qu’on calcule les p ⁿ et les q ⁿ connaissant les a ^k .

Les résultats essentiels de la théorie de ces fractions continuées sont les suivants:

(1) On a:

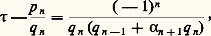ce qui montre que l’approximation de 精 par une réduite est d’autant meilleure que 見ⁿ⁺¹ est grand.

Par exemple 神 = [3, 7, 15, 1, 292, 1, 1, 1, ...] donne une excellente approximation classique p ³/q ³ = 355/113.

(2) Une condition nécessaire et suffisante pour que deux irrationnels 精 et 見 présentent, à partir de certains indices, les mêmes développements, est qu’ils soient liés par une transformation homographique modulaire , c’est-à-dire 靖 = (a 精 + b )/(c 精 + d ) avec ad 漣 bc = 梁 1 et a , b , c et d entiers.

(3) Une condition nécessaire et suffisante pour que 精 présente un développement périodique est que 精 soit un irrationnel algébrique du second degré (théorème dû à Lagrange).

pour tout n .

Sur deux réduites consécutives, l’une au moins vérifie:

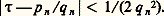Sur trois réduites consécutives, l’une au moins vérifie:

u /v est une réduite du développement de 精.

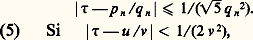(6) Si on développe le rationnel a /b en fraction continuée et si a /b = p ⁿ /q ⁿ , la réduite précédente (p ^n-1 )/(q ^n-1 ) fournit une solution de l’équation de Bezout:

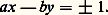(7) Si l’irrationnel 連d (d entier 閭 2) est développé en fraction continue, on a:

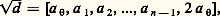périodique à partir de a ¹, période de n termes, avec a ¹ = a ^n-1 , a ² = a ^n-2 , ... (cela caractérise les développements de 連d ).

Si n est pair , les solutions de l’équation de Pell x ² 漣 dy ² = 1 sont données par x = p ^kn-1 , y = q ^kn-1 , pour k = 1, 2, 3, ... et x ² 漣 dy ² = 漣 1 n’a pas de solution.

Si n est impair les formules précédentes donnent: pour k = 1, 3, 5, 7, ..., les solutions de x ² 漣 dy ² = 漣 1, et, pour k = 2, 4, 6, ..., les solutions de x ² 漣 dy ² = 1. Par exemple x ² 漣 13 y ² = 1 conduit à:

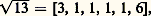d’où 649/180 pour k =2, donnant la plus petite solution x = 649, y = 180 qu’il était difficile de trouver par essais successifs.

Ces résultats s’établissent à partir de la formule:

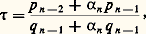relation modulaire liant 精 et 見ⁿ et exprimant que Dⁿ est sur (OD). On en tire en effet aussitôt la formule de (1) et le résultat de (2), qui, géométriquement, signifie qu’à partir d’une autre base du réseau Zⁿ les points de voisinage et les points réduits sont, assez loin, les mêmes qu’à partir de la base OA, OB; cela en raison du caractère géométrique intrinsèque des lignes polygonales de Klein. La condition nécessaire de (3) est évidente ( 見^k = 見^{k +} size=1^精 donne 見^k lié homographiquement – et même modulairement – à luimême, donc racine d’une équation du second degré; il en est de même pour 精). Sachant que 精 est irrationnel du second degré, on peut démontrer la condition suffisante. Algébriquement, en utilisant les équations du second degré que vérifient les 見ⁿ , équations à discriminant constant (ce qui permet, compte tenu de leurs signes, d’en limiter les coefficients; d’où répétition et période). On peut aussi le démontrer géométriquement, à partir de la rotation hyperbolique . Cette transformation consiste à associer à (OD) la demi-droite (OD ) correspondant au conjugué 精 de 精 et à remarquer que l’affinité d’axes (OD) et (OD ), et de multiplicateurs respectifs 益 et 益, où 益 est une unité de Q[ 精] de la forme u + c ²v 精 (u et v entiers, c ² coefficient du premier terme de l’équation définissant 精), conserve le réseau Z² et, par conséquent, fait «glisser» sur elles-mêmes, à partir d’un point suffisamment éloigné, les lignes polygonales de Klein relatives à (OD). Il y a donc période (et période dès le début si 精 礪 1 et 漣 1 麗 精 麗 0).

Les propriétés de (4) s’établissent en posant:

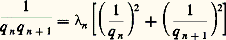et en montrant queⁿ ou^n-1 est inférieur à 1/ 連5, ce qui donne le résultat, grâce à:

La propriété (5) est évidente géométriquement, en considérant les parallélogrammes centrés en O, de côtés parallèles aux axes et dont un sommet est un point réduit.

La propriété (6) n’est autre que la récurrence fondamentale: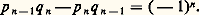

La propriété (7) est plus délicate à établir par le calcul; l’étude de

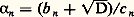conduit en effet à:

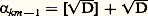et permet de conclure p ² 漣 q ² D = ( face=F0019 漣 1)^km pour la réduite d’ordre (km 漣 1). Reste à montrer qu’on a là toutes les solutions.

Signalons d’autre part que la propriété (2), qui n’est plus vraie lorsque la transformation n’est pas modulaire, est remplacée, lorsque ad 漣 bc = m 閭 2 par des formules assez simples de transformation des quotients incomplets, à condition que ceux-ci soient périodiques modulo m . C’est ainsi que le développement de

se transforme en:

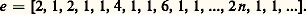Pour obtenir le développement de (e + 1)/(e 漣 1), Gauss a utilisé le développement en fraction continuée non régulière des séries hypergéométriques.

3. Approximations des irrationnels algébriques

On dit qu’un irrationnel 精 est rationnellement approchable à l’ordre 見 s’il existe une constante dépendant de 精, soit K( 精), telle que:

ait une infinité de solutions.

On voit sans peine qu’un rationnel u /v est approchable à l’ordre 1 et pas au-delà. D’autre part, les propriétés des fractions continuées montrent que tout irrationnel est approchable à l’ordre 2 au moins et qu’un irrationnel quadratique est approchable à l’ordre 2 et pas au-delà (à cause de la périodicité du développement). Ce dernier résultat est un cas particulier du théorème de Liouville (1844) relatif aux irrationnels algébriques de degré n : si 精 est de degré n , il n’est pas approchable à un ordre supérieur strictement à n . En effet, si f ( 精) = 0, où f est le polynôme de degré n définissant 精, l’étude de: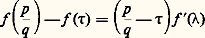

donne élémentairement:

pour tout rationnel p /q .

Le théorème de Liouville a une grande importance historique, puisqu’il a permis de définir explicitement les premiers nombres transcendants (nombres de Liouville), grâce à des développements (décimaux ou en fraction continuée) lacunaires tels que: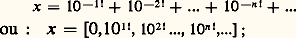

jusque-là on ne connaissait que l’existence des nombres transcendants (par complémentarité dans R des nombres algébriques) et ce n’est qu’en 1873 que Hermite établit la transcendance de e , permettant à Lindemann d’établir celle de 神 en 1882.

Le résultat de Liouville a été successivement amélioré par Thue (1908), établissant 見 諒 (n /2) + 1, par Siegel (1921) 見 諒 2 連n , par Dyson (1947) 見 諒 連2 n , et, en 1955, à l’aide d’une démonstration très technique, Roth améliorait définitivement le théorème: Tout irrationnel algébrique 精 est approchable à l’ordre 2 et pas au-delà. Cela permet d’affirmer par exemple que le développement décimal lacunaire x = 10^-1 + 10^-3 + 10^-9 + ... + 10^-3n + ... représente un nombre transcendant.

La recherche, pour un nombre algébrique 精, de la plus petite constante k ( 精), pour laquelle:

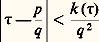a une infinité de solutions, est alors intéressante. Le nombre d’or :

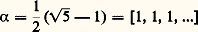a pour réduites les fractions de Fibonacci:

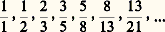et on voit aisément que:

ce qui montre que k ( 見) = 1/ 連5 (résultat de Hurwitz).

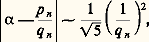Mais, si l’on excepte le nombre 見 et ceux qui lui sont équivalents par transformation modulaire, on peut établir que:

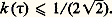Cela rejoint d’ailleurs les chaînes de Markoff-Hurwitz, qui, pour les irrationnels 精, étudient la limite supérieure M( 精) des constantes c telles que | 精 漣 (p /q )| = 1/(cq ²); on obtient M( 精) = 連5 pour le nombre d’or et ses équivalents, puis M( 精) 閭 2 連2 pour les autres irrationnels, avec M( 精) = 2 連2 pour 精 équivalent à 1 + 連2, puis M( 精) 閭 連221/5 pour les autres irrationnels, et ainsi de suite, les valeurs successives de M( 精) apparaissant étant données par la formule:

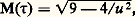où u = 1, 2, 5, 13, 29, ... est choisi de telle sorte que u ² + v ² + w ² = 3 uvw soit résoluble en entiers.

Citons encore deux résultats sur les approximations asymétriques. Ségré établit, en 1946, que, pour tout r 閭 0 et pour tout irrationnel 精, il existe une infinité d’approximations p /q telles que:

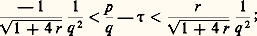le cas r = 0 donne la propriété (4) des fractions continuées et le cas r = 1 donne le résultat de Hurwitz. Robinson établit en 1947 que, pour tout 﨎 礪 0 et pour tout irrationnel 精, il existe une infinité d’approximations p /q telles que:

cela montre qu’on peut renforcer une des inégalités du théorème d’Hurwitz sans affaiblir beaucoup l’autre.

4. Approximations simultanées

Étant donné k irrationnels 精¹, 精², ..., 精^k , on peut soit chercher à les approcher par des fractions p ¹/r , p ²/r , ..., p ^k /r de même dénominateur (pas obligatoirement toutes irréductibles), soit chercher à rendre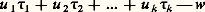

minimum pour des entiers u ⁱ et w . Ces deux problèmes duals l’un de l’autre sont également délicats. Le premier problème a été étudié initialement par Hermite, le second par Dirichlet. Une variante non homogène du deuxième problème consiste à rendre

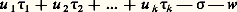minimum, 靖 étant donné non entier.

Un algorithme de Jacobi généralise pour les irrationnels l’algorithme des fractions continuées. Il correspond, pour k = 2, à:

où a ⁿ = [ 見ⁿ ] et b ⁿ = [ 廓ⁿ ], avec a ⁰ = [ 精] et b ⁰ = [ 靖].

Cela, géométriquement, ramène le premier problème d’approximation simultanée à l’exploration des points de Z³ autour de la demi-droite (OD) portant le vecteur de composantes ( 精, 靖, 1). On obtient une suite de points liés par la récurrence OP 轢ⁿ = OP^n-3+ b ⁿ OP^n-2+ a ⁿ OP^n-1et beaucoup de formules généralisent ce qui a été vu pour les fractions continuées. Malheureusement, si la convergence des réduites peut s’établir d’une manière générale, |p 漣 精 r | et |q 漣 靖 r | ne tendent pas toujours vers zéro. D’autre part, si on veut essayer de définir des points de voisinage, on doit tenir compte simultanément de | 精 漣 p /r | et | 靖 漣 q /r |, ce qui peut se faire par leur borne supérieure, leur somme, la somme de leurs carrés, et bien d’autres manières qui ne sont pas équivalentes entre elles. C’est pourquoi Hermite a pu dire que ce problème n’avait cessé, durant cinquante ans, de le préoccuper et de le désespérer.

Lorsqu’un développement de Jacobi pour k = 2 est périodique, il est facile de voir que 精 et 靖 sont deux éléments, non liés linéairement, d’un même corps cubique. La réciproque n’a pu être établie jusqu’à présent. Tout au plus peut-on dire, avec David (1956), que pour certains algorithmes voisins (où l’on prend par exemple a ⁿ = a ⁿ⁺¹ ou b ⁿ = b ⁿ + 1) cette réciproque est inexacte. Il n’en reste pas moins que d’intéressants résultats ont été obtenus par Perron grâce à l’algorithme de Jacobi, sur l’approximation de n entiers algébriques d’un corps de degré (n + 1).

Indépendamment de tout algorithme et par une simple application du «principe des tiroirs» de Dirichlet (Si n + 1 objets sont dans n tiroirs, l’un au moins de ces tiroirs contient plus d’un objet) on démontre qu’il y a au moins une solution au système | 精ⁱ 漣 p ⁱ /r | 麗 1/r ¹⁺ size=1^﨎, où 﨎 = 1/k . Ce résultat de Kronecker est sans grand intérêt dès que k dépasse 3. Par dualité, on en déduit que:

a des solutions entières u ⁱ et y , non toutes nulles, avec sup |u ⁱ | = t .

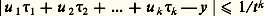Une étude plus précise de Kintchine lie l’indice 諸¹ de u ¹ 精¹ + u ² 精² + ... + u ^k 精^k 漣 y (c’est-à-dire la borne supérieure des 諸 tels que cette forme soit approchable à 1/t ^{k +} size=1^諸 près) à l’indice 諸² des k nombres 精ⁱ (c’est-à-dire la borne supérieure des 諸 tels que chaque 精ⁱ soit approchable à 1/t ¹⁺⁽¹⁺ size=1^諸)/k près).

On a:

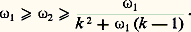Le cas non homogène (étude de | 精 p 漣 q 漣 靖|, ou, plus généralement, de | 精¹u ¹ + 精²u ² + ... + 精^k u ^k 漣 w 漣 靖|) a permis à Tchebycheff, Kintchine, Kronecker, Hermite et Minkowski d’obtenir des résultats analogues à ceux du cas homogène.

Signalons enfin d’intéressantes études sur l’approximation d’un nombre complexe 見 + i 廓 par le quotient P/Q de deux entiers de Gauss (Hermite, en liaison avec les formes quadratiques, Minkowski, Perron, Hurwitz en particulier). Un résultat essentiel est qu’il y a une infinité de solutions à

Le théorème de Thue-Siegel-Dyson-Roth sur l’approximation d’un irrationnel algébrique a été généralisé au cas de plusieurs irrationnels algébriques, en 1970, par W. Schmidt. Ainsi, pour 精¹, ..., 精ⁿ des nombres algébriques tels qu’aucune combinaison linéaire a ¹ 精¹ + ... + a ⁿ 精ⁿ , avec a ¹ , ..., a ⁿ rationnels non tous nuls, ne soit un nombre rationnel, et pour 﨎 réel positif arbitraire, il n’y a qu’un nombre fini d’entiers p ¹, ..., p ⁿ , q (q 礪 0) satisfaisant:

Plus généralement, désignant par 瑩x 瑩 la distance d’un réel x au plus proche entier, pour 精¹, ..., 精ⁿ et 﨎 comme ci-dessus, il n’y a qu’un nombre fini d’entiers positifs q tels que:

et il n’y a qu’un nombre fini d’entiers q ¹, ..., q ⁿ non nuls tels que:

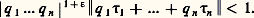5. Théorème de Minkowski et applications

Dans sa Géométrie des nombres , Minkowski établit en 1910 l’important théorème: Soit dans Rⁿ un domaine S convexe, borné, symétrique par rapport à O et de volume supérieur à 2ⁿ (ou égal à 2ⁿ si ce domaine est fermé). Ce domaine contient au moins un point entier distinct de O (il contient donc aussi son symétrique par rapport à O).

La démonstration utilise l’homothétique S de S dans l’homothétie (0, 1/2). Pour un entier m assez grand, soit le réseau (Z/m )ⁿ des points de coordonnées x ⁱ = u ⁱ /m où u ⁱ 捻 Z. Soit N(m ) le nombre d’hypercubes de côtés 1/m de ce réseau qui sont dans S . On a N(m ) 憐 m ^s aussi voisin qu’on veut de 1/2ⁿ . V(S) pour m assez grand et cela permet d’affirmer l’existence de deux sommets où les u ⁱ et u ⁱ sont congrus modulo m , pour i = 1, 2, ..., n . Le vecteur joignant ces deux sommets est donc un point entier, car (u ⁱ 漣 u ⁱ )/m est entier, qui appartient à S + S = S.

L’application essentielle de ce théorème concerne la résolution des systèmes d’inéquations diophantiennes:

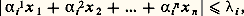pour i = 1, 2, ..., n , où les 見^{i j} sont réels donnés, ainsi que lesⁱ , et dont on cherche des solutions entières non banales (x ⁱ entiers non tous nuls). Ces inéquations définissent une jauge de Minkowski (c’est ainsi qu’on appelle les domaines S définis ci-dessus) dont le volume est 2ⁿ¹² ...ⁿ /| |, où est le déterminant des 見^{i j} . On peut donc affirmer que, si¹² ...ⁿ 閭 | |, il y a des solutions entières, autres que le point O, au système des n inéquations. En particulier, on retrouve le résultat de Kronecker: le système de n inéquations

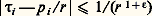est résoluble pour 﨎 = 1/n ; en effet, cela s’écrit:

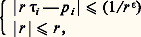système de (n + 1) inéquations résoluble puisque la condition de Minkowski est ici réalisée:

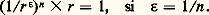On peut d’ailleurs, si les 見^{i j} sont entiers, appliquer ces résultats à des systèmes d’équations linéaires, car:

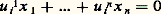équivaut à:

si les u ^{i j} sont entiers et si l’on cherche à résoudre en entiers x ⁱ .

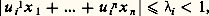Le théorème de Minkowski s’étend de plus au cas complexe, à condition que les inéquations du système soient réelles ou imaginaires conjuguées 2 à 2 (avec alors le mêmeⁱ pour ces deux inéquations). Il vient encore la condition¹² ...ⁿ 閭 | |, suffisante pour entraîner l’existence de solutions entières autres que le point O. C’est sous cette forme que le théorème permet la démonstration d’un important théorème de Dirichlet sur l’existence des unités dans une extension algébrique de Q.

On peut aussi appliquer le théorème des jauges de Minkowski en définissant celles-ci par: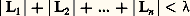

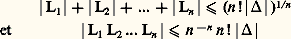où Lⁱ = 見^{i 1}x ¹ + ... + 見^{i n} x ⁿ . On démontre ainsi que les deux inéquations:

ont l’une et l’autre des solutions non banales, car:

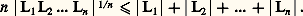On peut toutefois noter que, contrairement au cas des inéquations, où la condition |¹² ...ⁿ | 閭 | | ne peut être améliorée d’une manière générale, on peut parfois améliorer les résultats ci-dessus. Par exemple, pour n = 2, on peut affirmer que l’inéquation |L¹ L²| 諒 | | 連5 admet toujours des solutions non banales.

La réduction des formes quadratiques utilise aussi le théorème de Minkowski, appliqué à L¹² + L²² + ... + L^{n 2}.

Blichfeldt (1914) a étendu à d’autres domaines que des jauges les méthodes de Minkowski; ces recherches ont été poursuivies par Mordell, Davenport et Mahler.

6. Répartition modulo 1

Quoiqu’il ne s’agisse pas à proprement parler d’approximation diophantienne, on peut ranger dans cet article l’étude des suites de nombres réels, modulo 1. Il s’agit, pour une suite (u ⁿ ), de la répartition sur [0, 1[ deu ⁿ = u ⁿ 漣 [u ⁿ ] où [u ⁿ ] est la partie entière de u ⁿ .

Ce n’est qu’en 1884 que Kronecker établit que, si est irrationnel, ses multiples n sont, modulo 1, partout denses sur [0, 1[. Cela signifie que, quel que soit x 捻 [0, 1[ et quel que soit 﨎 礪 0, il existe une infinité de valeurs de n pour lesquelles |n 漣 x | 麗 﨎. En effet,n ¹ est différent den ² si n ¹ n ²; il existe donc au moins un point d’accumulation des nombres (n ), c’est-à-dire qu’on peut trouver n ¹ et n ² avec (n ¹ 漣 n ²) 捻 ]0, 﨎[, d’où les multiples m (n ¹ 漣 n ²) qui fournissent des points, modulo 1, à moins de 﨎 de tout x de [0, 1[.

On remarquera que le problème de la répartition sur un cercle des points d’abscisse curviligne n conduit au même résultat si est incommensurable à 神 (ici on raisonne modulo 2 神). De même, par exemple, l’étude des premiers chiffres du nombre 2ⁿ , écrit en base 10, conduit à étudier la mantisse de n log 2, c’est-à-dire sa répartition modulo 1. Comme log 2 est irrationnel, puisque 10^{p /q} 2, on en déduit qu’on peut toujours trouver une infinité de valeurs de n telles que 2ⁿ commence par k chiffres quelconques imposés.

La notion d’équirépartition fut mise au point par Weyl en 1916. La suite (u ⁿ ) est dite équirépartie modulo 1 si lesu ⁿ sont denses sur [0, 1] et si, de plus, pour tout [ 見, 廓] 說[0, 1] le nombre 﨏^N( 見, 廓) d’indices n pour lesquels n 諒 N etu ⁿ 捻 [ 見, 廓] vérifie: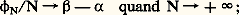

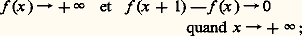une condition suffisante pour que la suite (f (n )) soit dense sur [0, 1[ est que:

c’est ainsi que la suite ( Log^a n ) est dense sur [0, 1[ modulo 1, quel que soit le nombre réel non nul et le nombre réel a 礪 1.

Dès 1912, Bohl, Sierpinski et Weyl établissent l’équirépartition de (n ) pour irrationnel cependant que Fejer donne des conditions suffisantes d’équirépartition ou de non-équirépartition: Si f est strictement croissante, à dérivée continue monotone, avec f (x )+ 秊, f (x )0, xf (x )秊 quand x+ 秊, il y a équirépartition. Si au contraire xf (x )0, il n’y a pas équirépartition. On en déduit les résultats concernant ( Log^a n ) (équirépartition si a 礪 1, non-équirépartition si a 諒 1). En 1916, Weyl énonce le critère d’équirépartition: celle-ci est caractérisée, pour une suite f (n ), par le fait que, pour tout entier h non nul,

est un o(n ) pour n秊.

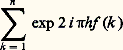Plus tard (1933), Koksma établit que la suite t ⁿ , où est réel non nul fixé, est équirépartie modulo 1 pour presque tous les t 礪 1 (mais on ne connaît aucun t pour lequel on ait établi cette équirépartition; on pense par exemple que (3/2)ⁿ est équiréparti modulo 1, mais on n’a pas pu le démontrer jusqu’ici). En revanche, une catégorie importante de nombres algébriques échappe à cette équirépartition: il s’agit des nombres de Pisot-Vijayaragavan, qui sont des entiers algébriques tels que 礪 1, les conjugués ⁱ , pour i = 2, 3, ..., s (s est le degré de ), étant tous en modules inférieurs à 1. Il s’ensuit que ⁿ converge vers zéro modulo 1 (raisonner sur ⁿ + ^{n 2} + ... + ^{n s} qui est un entier). Salem a démontré en 1944 que l’ensemble S des nombres de Pisot était fermé.

Encyclopédie Universelle. 2012.